Dedekind , (Julius Wilhelm) Richard
- Dedekind , (Julius Wilhelm) Richard
(1831–1916) German mathematician
The son of an academic lawyer from Braunschweig, Germany, Dedekind was educated at the Caroline College there and at Göttingen, where he gained his doctorate in 1852. After four years spent teaching at Göttingen, he was appointed professor of mathematics at the Zürich Polytechnic. In 1862 he returned to Braunschweig to the Technical High School where he remained until his retirement in 1912.
In 1872 Dedekind published his most important work Stetigkeit und Irrationale Zahlen (Continuity and Irrational Numbers) in which he provided a rigorous definition of the irrational numbers. He began by ‘cutting’ or dividing the rational numbers into two non-empty disjoint sets A and B such that if x belongs to A and y toB, then x łe; y. If A has a greatest member A' then A' is a rational number; if B has a smallest number B' then B' will also be a rational number. But if A has no greatest number and B no smallest, then the cut defines an irrational number.
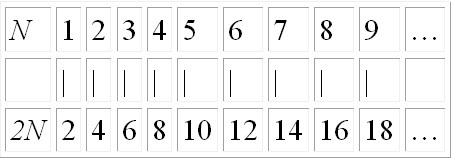
In the same work Dedekind gave the first precise definition of an infinite set. A set is infinite, he argued, when it is “similar to a proper part of itself.” Thus the set N of natural numbers can be shown to be ‘similar’, that is, matched or put into a one-to-one correspondence with a proper part, in this case 2N:
Whereas the only thing a finite set can be matched with is the set itself.
In a later work,
Was sind und was sollen die Zahlen? (What numbers are and should be, 1888) Dedekind demonstrated how arithmetic could be derived from a set of axioms. A simpler, but equivalent version, formulated by
Peano in 1889, is much better known.
Scientists.
Academic.
2011.
Look at other dictionaries:
Julius Wilhelm Richard Dedekind — Richard Dedekind fundamentó la teoría de la recta real y creó la teoría de los ideales Julius Wilhelm Richard Dedekind (6 de octubre de 1831 12 de febrero de 1916), matemático alemán. Dedekind nació en Brunswick (Braunschweig en alemán), el más… … Wikipedia Español
Julius Wilhelm Richard Dedekind — (6 de octubre de 1831 12 de febrero de 1916), matemático alemán. Dedekind nació en Brunswick (Braunschweig en alemán), el más joven de los cuatro hijos de Julius Levin Ulrich Dedekind. Vivió con Julia, su hermana soltera, hasta que falleció en… … Enciclopedia Universal
Dedekind — (Julius Wilhelm) Richard … Scientists
Richard Dedekind — Infobox Scientist name = PAGENAME box width = image size =180px caption =Richard Dedekind, c. 1850 birth date = October 6, 1831 birth place = Braunschweig death date = February 12, 1916 death place = Braunschweig residence = citizenship =… … Wikipedia
Richard Dedekind — Naissance 6 octobre 1831 Brunswick … Wikipédia en Français
Dedekind — Dedekind, 1) Friedrich, Dichter, * Neustadt am Rübenberge um 1525, ✝ Lüneburg 21. 2. 1598; Pastor. Dedekind wirkte weniger durch seine deutschen Dramen »Der christliche Ritter« (1576) und »Papista conversus« (1596), in denen er die… … Universal-Lexikon
Richard Dedekind — Porträt (1850) Julius Wilhelm Richard Dedekind (* 6. Oktober 1831 in Braunschweig; † 12. Februar 1916 ebenda) war ein deutscher Mathematiker. Inhaltsverzeichnis … Deutsch Wikipedia
Dedekind — /day di kind/; Ger. /day deuh kint/, n. Julius Wilhelm Richard /joohl yeuhs wil helm rich euhrd/; Ger. /yooh lee oos vil helm rddikh ahrddt/ 1831 1916, German mathematician. * * * … Universalium
Dedekind — /day di kind/; Ger. /day deuh kint/, n. Julius Wilhelm Richard /joohl yeuhs wil helm rich euhrd/; Ger. /yooh lee oos vil helm rddikh ahrddt/ 1831 1916, German mathematician … Useful english dictionary
Julius Dedekind — Julius Levin Ulrich Dedekind (* 11. Juli 1795 in Holzminden; † 2. August 1872 in Braunschweig) war ein deutscher Jurist. Er lehrte von 1822 bis 1872 am Braunschweiger Collegium Carolinum, dessen Entwicklung er erheblich mitbestimmte.… … Deutsch Wikipedia
Whereas the only thing a finite set can be matched with is the set itself.In a later work, Was sind und was sollen die Zahlen? (What numbers are and should be, 1888) Dedekind demonstrated how arithmetic could be derived from a set of axioms. A simpler, but equivalent version, formulated by Peano in 1889, is much better known.